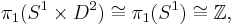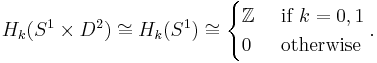Solid torus

In mathematics, a solid torus is a topological space homeomorphic to 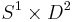$S^1 \times D^2$ , i.e. the cartesian product of the circle with a two dimensional disc endowed with the product topology. The solid torus is a connected, compact, orientable 3-dimensional manifold with boundary. The boundary is homeomorphic to 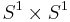$S^1 \times S^1$ , the ordinary torus.

A standard way to picture a solid torus is as a toroid, embedded in 3-space.

Since the disk 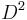$D^2$ is contractible, the solid torus has the homotopy type of 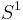$S^1$ . Therefore the fundamental group and homology groups are isomorphic to those of the circle:

$\pi_1(S^1 \times D^2) \cong \pi_1(S^1) \cong \mathbb{Z},$

$H_k(S^1 \times D^2) \cong H_k(S^1) \cong \begin{cases} \mathbb{Z} & \mbox{ if } k = 0,1 \\ 0 & \mbox{ otherwise } \end{cases}.$

See also